A poignant moment arises in Stand and Deliver, a film about a group of students at Garfield High School in East Los Angeles whose lives are changed by their mathematics teacher, Jaime Escalante. He has finally begun to connect with them. With wide smiles they are following his lead in repeating a standard algebraic rule: "A negative times a negative equals a positive." After several rounds of this chant there is a pregnant pause, after which Mr. Escalante—with an equally wide smile—asks, "Why?"

The camera then cuts to another scene, leaving the question unanswered. Some in the viewing audience may very well wish that the scene had continued, having remembered the rule but forgotten the explanation. Indeed, why does a negative times a negative equal a positive? Most people have accepted this maxim even if they never heard a good explanation for it. After all, the laws of algebra have the same status as the laws that came down on a tablet from Mount Sinai, don't they?

Well, no, at least not according to Alberto Martínez, whose Negative Math: How Mathematical Rules Can Be Positively Bent is at once scholarly and readable. He argues that many of the rules of algebra could have been otherwise. The adopted ones came about by a variety of factors, and don't necessarily offer the best resource for dealing with every kind of scientific inquiry.

This attitude may seem odd: many thinkers view numerical theorems as independent of human construction. In the words of Martin Gardner, "If two dinosaurs met two others in a forest clearing, there would have been four dinosaurs there—even though the beasts were too stupid to count and there were no humans around to watch."

Interestingly, this opinion of mathematical independence may not be so widely held with respect to the theorems of geometry. The Kantian view that our minds are equipped with a category of (Euclidean) space—a category that exists inside us as a condition of knowledge—likely dissipated with the advent of non-Euclidean geometries in the mid 1800s. But a general conviction that our minds have a category of quantity—necessary for the perception of real things—seems to hold sway with the general public.

When the absolute truth of geometry fell from grace, mathematicians became bolder in thinking that deviant algebraic constructs—hitherto deemed as nonsensical because they did not correspond with geometric ideas—could seriously be considered. In this spirit Martínez, although steering clear of abstract philosophical discussions, wants to show that even well-established algebraic axioms might be altered, especially those that do not fully match our experience.

The first part of Martínez's book contains a sweeping survey of the historical development of algebraic systems, concentrating on the problems of dealing with negative quantities. Some readers may be surprised to learn that serious discussion of negative numbers spanned several centuries—from at least Girolamo Cardano's publication of Ars Magna (Great Art) in 1545, to Augustus De Morgan's On the Study and Difficulties of Mathematics, published in 1831. Even into the 1880s, imaginary numbers (quantities dealing with the square root of minus one) had dubious status at Cambridge University.

Martínez writes in an informal style: "If later tonight you go to sleep and tomorrow somehow forget everything else in these pages, then at least please remember this." He treats his readers to quotations from PhD theses, textbooks, journal articles, and letters, not mention remarks from many central mathematical and philosophical figures (Berkeley, Cauchy, Comte, d'Alembert, Dedekind, Einstein, Euler, Gauss, Hamilton, Kant, Leibniz, Newton, Russell, and Wallis, among others), all of whom had something to say about negative numbers.

So what is it that we are supposed to remember? Basically, that there is a conceptual difference between the signed numbers +4 and –4, and the signless number 4, just as a displacement of 4 steps to the right (+4), or to the left (–4) is not the same as a distance of 4 (signless) units. For Martínez, ordinary numerical methods do not capture this physical distinction. There are two additional points to remember: first, negative numbers, at least in part, grew out of abstractions from concrete numerical operations, such as 5 – 2 = 3, to symbolic representations, such as a – b = c; second, mathematics continues to be flexible. In some very real ways it may make sense to stipulate that a negative times a negative equals a negative.

Indeed, even though most teachers can give plausible physical analogies in support of the "Escalante" rule, Martínez argues that there is an intrinsic asymmetry in it, one that would be erased if a negative times a negative equaled a negative. How is this so? Consider the standard "number line," with zero at the center and the (signed) numbers in their usual positions, as shown in the following diagram.

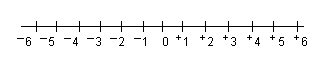
Multiplying together two numbers to the right of zero, say +2 by +3, gives +6, effectively moving +2 (the original number) a total of 4 (signless) units to the right. Why is it, Martínez asks, that numbers to the left of zero, when multiplied together, don't get displaced further to the left? As things now stand, multiplying –2 by –3, also gives +6, displacing –2 (the original number) a distance of 8 (signless) units to the right. If, instead, –2 times –3 equaled –6, the original number –2 would be displaced 4 (signless) units to the left, giving perfect (bilateral) symmetry.

But hasn't it been proven that the Escalante multiplication rule is valid? Yes, but it's been proven relative to certain assumptions, which Martínez says can be freely called into question. The main change he proposes is that the product of two numbers gets the sign of the first number. Thus, the product of two positives remains positive, but the product of two negatives is now negative. Besides restoring bilateral symmetry to multiplication, Martínez's rule would abolish the need for imaginary numbers: the square root of minus one would simply be minus one, because (⁻1)2 = ⁻1.

Of course, there are disadvantages to this proposed change: the commutative law would no longer hold. This law states that the order in which we multiply numbers does not matter, i.e., the product ab is the same as the product ba. Under Martínez's scheme we would now have ⁻2 x ⁺3 = ⁻6, but ⁺3 x ⁻2 = ⁺6.

Martínez confesses that the commutative law is a good one for products of positive numbers, and also for products of negative numbers. But why, he asks, must we think it necessary that the law should hold with (mixed) products of positive and negative numbers? After all, many mathematical operations are not commutative. For example, division is not commutative because 6 ÷ 3 = 2, but 3 ÷ 6 = 1/2. Martínez's point is weak here because the property of commutativity (or lack thereof) in the examples he cites depends on the operation itself (multiplication or division), and not on the numbers that are being manipulated by the operation. He might strengthen his argument with a physical analogy like the following:

Take a book and place it flat on a table, so that you would open it in the usual way. Now consider two types of orientation changes you might make to the book: rotations and flips. The commutative law holds if rotations are followed by rotations, or flips are followed by flips. As confirmation, rotate the book by 90 degrees, then by 180 degrees. The same result occurs if you first rotate the book by 180 degrees, then by 90 degrees. Commutativity does not hold, however, if rotations and flips are combined: rotate the book 90 degrees counter clockwise (so that the binding is facing you); next, flip the book 90 degrees away from you (so that the binding is pointing towards the ceiling). Return the book to its original starting position and reverse these moves (i.e., perform a flip followed by a rotation). You'll discover that the binding is pointing toward you, a completely different result.

The second part of Martínez's book details case studies of what might result from tinkering with the standard rules of mathematics. The reader may find it difficult to wade through his litany of examples, some of which seem a bit contrived. What is the main point Martínez wants to make in producing them? It is to reinforce a general theme that permeates his book: the rules of mathematics are flexible.

Flexible, yes; arbitrary, no, and one might criticize Martínez for leaving us with the latter impression. In fact, the drawbacks he sees in the standard rules of multiplication are overstated, and he understates the disadvantages that would result if his proposed system were adopted.

To illustrate, recall Martínez's claim that the Escalante multiplication rule lacks symmetry. It indeed lacks the bilateral symmetry that he described, but it has, from the standpoint of complex analysis, a perfect rotational consistency to it. Ironically, later in his book, Martínez defends the lack of bilateral symmetry in a graph generated with his new system by claiming that, though it fails to have bilateral symmetry, it exhibits rotational symmetry.

What is this rotational symmetry or consistency? Complex analysis represents numbers as points on the xy coordinate system. Except for the origin itself, they reside at a location determined by a certain distance from the origin as well as an angular rotation measured from the positive x-axis, as illustrated by the numbers r (distance) and Θ (rotation) below.

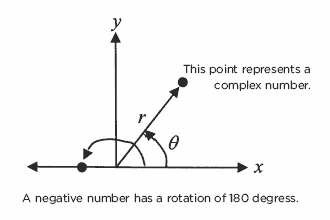
To multiply numbers in complex analysis, one simply multiplies their distances, and adds their rotations. Thus, two negative numbers, each with an angular rotation of 180 degrees, combine to give a result that is rotated a total of 360 degrees, coinciding with the positive x-axis. Two positive numbers, by contrast, each have a rotation of zero degrees. When multiplied, the resulting value stays on the positive x-axis. From the standpoint of rotations, then, everything is perfectly consistent.

There are other occasions where Martínez demonstrates some mathematical ignorance. For example, he points out that, with his proposed multiplication rules in place, the equation y = x³ + 2x² – 8x generates a different graph than does y = x3 + 2x2 – x8. Why? Because the number 8x is always positive (since the number 8 is positive), whereas x8 has the same sign as x. The switch effectively alters the equation. He then claims, "We are able to construct a variety of curves that otherwise have no algebraic representation." But the absolute value construct can produce curves that have the same effect: the quantities 8x and 8|x| with the Escalante rule are equivalent, respectively, to x8 and 8x with Martínez's scheme. His claim, then, simply does not hold up.

Even more problematic is that abstract mathematical manipulations would be stymied with Martínez's rules. Without going into technical details, the basic problem stems from the fact that the right-sided distributive law—(a+b)(c) = ac + bc—is no longer valid. Martínez admitted, after some email exchanges, that this deficiency was a serious obstacle. His book, though, leaves the opposite impression.

It may be for these reasons that some in the mathematical community have reacted quite negatively to Martínez's book. One reviewer went so far as to say that there is nothing worthwhile in it. Such criticisms are unfair: Martínez is not seriously proposing the adoption of a new multiplication system. His aim, rather, is to encourage the development of mathematical systems that match physical reality: "We should carefully study the symbolic and procedural methods we employ as tools of physical representation and analysis." Martínez took on this project because he believes that textbooks do not usually discuss how algebra was put together. He thinks that students of science should realize that they can adapt mathematics to fit their discipline. They should do more than merely apply what has been handed down to them, even if the old rules for multiplying two negatives hold together.

So why does a negative times a negative equal a positive? A complete answer to this question is beyond our purpose here. A short reply is that the rule is required to keep mathematical manipulations consistent: if we agree that any number times zero equals zero, then (⁻1) (0) = 0. But this expression can also be written as (⁻1)( ⁺1 + ⁻1) = 0, so by the distributive law (⁻1)( ⁺1) + (⁻1 )( ⁻1) = 0. If we also agree that (⁻1)( ⁺1) = ⁻1, the expression (⁻1 )( ⁻1) in the previous equation must equal ⁺1.

Does this outcome render the reading of Negative Math pointless? In answering this question we might refer to a remark by Ludwig Wittgenstein. He writes (Philosophical Investigations, Aphorism 67):

Why do we call something a "number"? Well, perhaps because it has a—direct—relationship with several things that have hitherto been called number; and this can be said to give it an indirect relationship to other things we call the same name. And we extend our concept of number as in spinning a thread we twist fiber on fiber. And the strength of the thread does not reside in the fact that some one fiber runs through its whole length, but in the overlapping of many fibers.

Besides being exposed to a piece of mathematical history, those reading Negative Math may have their imagination expanded. Some may even be led to generate new golden fibers that can be used in weaving the fabric of mathematics.

Russell W. Howell is professor of mathematics at Westmont College. With John H. Mathewes, he is the author of Complex Analysis for Mathematics and Engineering (Jones & Bartlett, 5th ed.).

Copyright © 2009 by the author or Christianity Today/Books & Culture magazine.
Click here for reprint information on Books & Culture.